Project Euler is a series of increasingly difficult Mathematical questions/puzzles that tends to scratch the problem solving itch that many programmer are afflicted with. While they can usually be brute forced via computer programs usually they have an elegant solution that can be worked out with just a pencil and paper. As such at least for programmers it really is up to the individual how much deep thought versus straight coding they want to do, which, I think makes for a pretty good learning curve. When you cant figure out the elegant solution, you can usually find a brute force way through it; When you cant brute force it, you have to sit back, think and usually you can come up with an elegant efficient way to solve the problem. This is pretty similar to the real life challenges in programming really get resolved, first try to come up with a ‘good’ way to do things, if not then just resolve it by brute force, finally when necessary put in deep thought and or research to really find an efficient solution.
So with that being said, going to look at Euler Problem #1:
If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23. Find the sum of all the multiples of 3 or 5 below 1000.
I remember in fifth grade, my math teacher showed us a very small Basic program (no clue which specific Basic, but it ran on MS-DOS so…) that would count up to 1 million and print the numbers to the screen. The most awe inspiring part of the lesson was not the program, but the fact that he had to leave the program running until the next day in order for it to complete. Really impressed upon us not only the power of computer programs, but also the shear immensity of the number 1 million. Big ups to Mr Weinstein. I tried to recreate the experience for my son a few years ago, but alas the program finished REALLY quickly. I guess that comes down to Moore’s law spoiling the awesomeness of the number 1,000,000, let alone 1000.
So in honor of these realities, and because I also want to look at some basic performance comparisons across languages, and in celebration of the inventors of the most powerful and important computing system in the history of the earth lets bump that 1000 up to 10,000,000 (a crore). An before anyone questions wether Hindu-Arabic is arguably the most important computing system invented by humankind, quick tell me what is MCMLXXXVII divided by XVIII? I’ll wait, might take a couple hours for you to work out if you dont convert to a place value based system with a representation of zero that allows finite mechanical application of a small set of basic rules to resolve long division. Long division doesn’t just fall out of all number systems. This number system is what made calculation, beyond hands and toes possible for the vast majority of society. So for the shear democratization of arithmetic and advancement of mathematics both practical and academic that this system allowed, I think it easily ranks as number 1 computing system in human history. But I digress…
Let’s get down the summing up all the multiples of 3 or 5 below 10,000,000.
PowerShell
$max = 10000000 - 1
$sum = 0
1..$max |
? { (( $_ % 3 ) -eq 0) -or (($_ % 5) -eq 0) } |
% { $sum += $_ }
$sum
Kind of painful to read, and this is not even the most compressed way to write this in PowerShell. I actually added line breaks and broke out the sum variable to make it a little easier to read. Being 100% fair, the syntax of powershell is optimized for quick input of ‘fire and forget’ dispatches at the command line. Every ugly weird magically shortcut here, I wouldnt trade away from the language at all because of the speed at which you can crank out PowerShell one liners. But its still ugly and hard to read.
I checked the performance with hyperfine. Why? Well programs execution is fairly nondeterministic. It can depend on a hundred different things, mostly commonly related to caching/optimizations that the program runtime has made, or contention for resources during execution. As such it is often necessary to let the code execute a bit to ‘warm up’ and then also to actually execute a reasonable number of times to determine the average run time and variance. hyperfine does this kind of thing for you, without having to do any special coding on your part. The results looked like below:
❯ hyperfine 'pwsh .\powershell\euler.ps1'
Benchmark #1: pwsh .\powershell\euler.ps1 0
Time (mean ± σ): 135.411 s ± 3.449 s [User: 0.0 ms, System: 5.1 ms] 0
Range (min … max): 131.319 s … 142.754 s 10 runs
Which is pretty significantly slow run on modern hardware clock in at over 2 minutes. I wasnt able to find incredible detail on how PowerShell actually executes, but at a minimum I know there is an interpreter that does a LOT of dynamic indirection related to PSObject and PSCustomObject, and then calls down to .Net code that has to be compiled down (I am assuming) to Microsoft Intermediate Language, and then on execution that MSIL has to be JIT’ed (Just In Time converted) to native machine code. It seems at least niavely that this has to be on a line by line basis to enable PowerShell to function as a shell. As such I wasnt surprised it was slow but how slow is slow?
I was curious to see how another ‘slow’ interpreted language peformed:
Python
max = 10000000
sum = 0
for i in range(1, max):
if i%3==0 or i%5==0:
sum += i
print(str(sum))
Wow so much more readable, I think perhaps a complete non programmer could look at this and have a decent idea of what is going on, only real headscratchers would be the % modulus functions, the == and += symbol.
❯ hyperfine 'python .\python\euler.py'
Benchmark #1: python .\python\euler.py 0
Time (mean ± σ): 1.100 s ± 0.036 s [User: 2.9 ms, System: 6.2 ms] 0
Range (min … max): 1.065 s … 1.147 s 10 runs
Whats widely regarded as the slowest mainstream programming language is over 100 times faster on this microbenchmark. Even in the realm of popular interpreted dynamic languages such as JavaScript, Lua, Perl, Python is considered dog slow. And lets be crystal clear here:
Microbenchmarks mean nothing to anything except the very specific exact lines of code in question
But still 2 orders of magnitude faster, on very simple looping and integer arithmetic.
That got me much more curious, what about a decently performant programming language? C# is a relatively performant statically typed compiled language that executes on a virtual machine with a garbage collector.
C#
using System;
namespace euler_dotnet
{
class Program
{
static void Main(string[] args)
{
int max = 10000000;
Int64 sum = 0;
for(int i=0; i < max; i++)
{
if(((i % 3)==0)||((i % 5)==0))
{
sum += i;
}
}
Console.WriteLine(sum.ToString());
}
}
}
First thing we are going to notice looking at the code is how verbose it is, probably 50% of the code is just boilerplate that really has nothing to do with the actually problem we are trying to solve. It is an extremely explict language, thats for sure. Lets see how it performs though.
❯ dotnet build --configuration Release .\dotnet\
❯ hyperfine 'python '.\dotnet\bin\Release\netcoreapp3.1\euler.exe'
Benchmark #2: .\dotnet\bin\Release\netcoreapp3.1\euler.exe
Time (mean ± σ): 56.5 ms ± 0.6 ms [User: 0.9 ms, System: 2.9 ms] 0
Range (min … max): 55.9 ms … 59.6 ms 46 runs
About 19 times faster than Python off rip. Maybe the trade off between verbosity and performance is worth it. If we are being REALLY fair we also should note the build step, thats the lines that go dotnet build etc. The build step does eat up time on its own. Especially in exploritory development the constant code, build, wait, execute cycle really does slow down development when you take into account a developer does this cycle hundreds of times a day. Both Python and PowerShell, just do the magic to make your code actually execute at runtime.
I wanted to go one level deeper, and see how a language that compiles down to a single native executable that doesnt depend on a garbage collector. I chose Rust because, frankly last time I tried to teach my 16 year old son C, it blue screened my computer. So lets try the much safer low level language that has been stackoverflow’s Most Loved Programming Language for 3 years in a row.
Rust
fn main() {
let max = 10000000;
let mut sum = 0i64;
for i in 1..max {
if i % 3 == 0 || i % 5 == 0 {
sum += i;
}
}
println!("{}",sum);
}
Before we even run it, stands out that it is pretty near to python in readability, sure there are semicolumns everywhere, and the weird 0i64 but… not anywhere as ugly as PowerShell, nor as long winded as C#.
How does it run though?
❯ cargo build --manifest-path .\rust\Cargo.toml --release
❯ hyperfine '.\rust\target\release\euler.exe'
Benchmark #1: .\rust\target\release\euler.exe 0
Time (mean ± σ): 15.5 ms ± 0.2 ms [User: 1.0 ms, System: 3.8 ms] 0
Range (min … max): 15.0 ms … 16.1 ms 143 runs
So about 3.6 times faster than C#, about 70 times faster than Python, and about 9,000 times faster than PowerShell. Thats pretty fast. Must be pretty much as fast as possible right?
Math
This series is tagged comp-sci for a reason, so lets try to apply the Queen of the Sciences to help speed up this calculation for us.
What’s our overall strategy for solving this problem?
Lets try to divide and conquor this problem by breaking it down into simpler problems. An obvious first step is with the multiples of 3:
3 + 6 + 9 + 12 + 15 + … up to whatever the largest multiple of 3 is thats less than 10,000,000
I can make a reasonable guess for the largest multiple of 3 less than 10,000,000 just off the top of my head, but I wouldn’t necessarily know ‘how’ I figured it out.
When in doubt go back to first principals. What’s the definition of the terms you are using?
The largest multiple of 3 less than 10,000,000 is literally the largest number less than 10,000,000 that can be divided by 3 perfectly. Lets start with 10,000,000/3 = 3,333,333.333333… the decimal is the part that didnt perfectly divide. So just throwing that away by rounding down we get 3,333,333. If we multiply by 3 x 3,333,333 we get 9,999,999 as the largest multiple of 3 thats less than 10,000,000.
We didnt use any special properties of the number 3 or 10,000,000 to get here, so this seems to be a general rule: The largest multiple of any number (Y) less than some number (MAX) is always going to be = Y times the whole number part of MAX/Y. The round down function is often in programming languages called the’floor’ and multiplication is commonly shown in programming languages by the symbol ‘*’. So Y * floor(MAX/Y).
Can we check that this is valid?
Lets apply this to find out what the largest multiple of 5 less than 10,000,000 is by applying the formula 5 * floor(10,000,000/5) = 10,000,000. Which is NOT less than 10,000,000. Turns out that we were using a special property of 3 ad 10,000,000, that 3 doesn’t evenly divide 10,000,000. We can patch this edge case by just subtracting 1 from the MAX to guarantee we truly only look for multiples less than MAX.
multiple of Y less than MAX = Y * floor((MAX-1)/Y)
Back to our problem:
3 + 6 + 9 + 12 + 15 + … + 9,999,999 still is a mystery. Maybe we can find some form of this sequence that is more basic? At its simplest it just the 3 multiplication table:
3 * 1 + 3 * 2 + 3 * 3 + … 3 * 3,333,333 = 3 * (1 + 2 + 3 + 4 + 5 + … 3,333,333)
This seems like we are going in the right direction its not clear how to move on from here. A really powerful tool in problem solving is visualizing the problem. Why is this so powerful? It turns out something like 2/3rds of the human brain is involved in the processing of visual information, and almost all of our intuition for judging relationships between proportions is especially tied to vision.
So when I am stuck I always start with sketching an quick diagram to visualize the problem i am trying to solve.
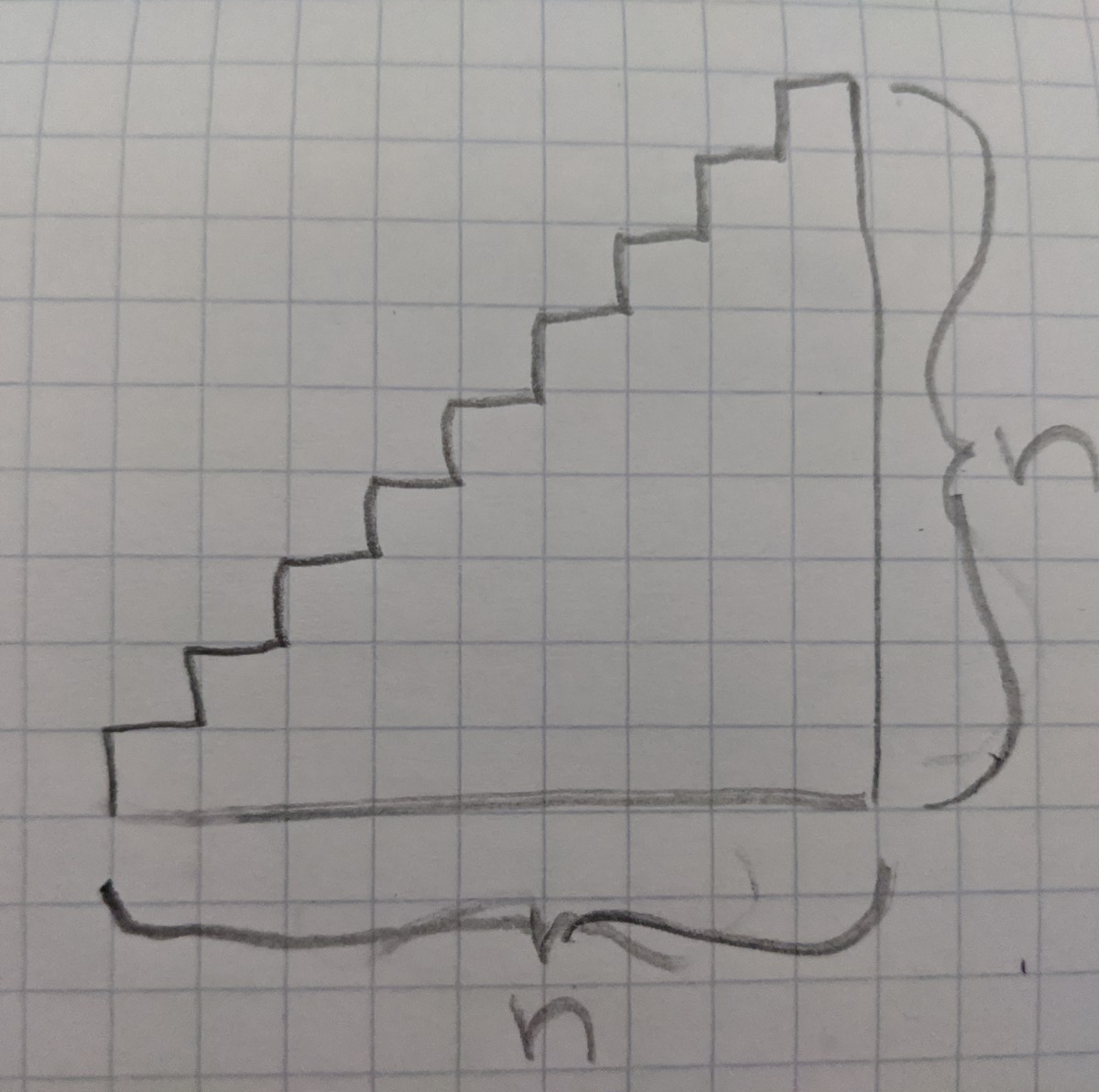
Immediately it jumps out that the sequence 1 + 2 + 3 + 4 + … + n forms a stairway shape. If we could just figure out a formula for inside the stairway shape, we would have a formula to caluculate the sum of integers from 1 to n.
Does this problem look like a simplier problem I know how to solve already?
The most obvious thing my intuition sees is that this looks like a triangle, so let me draw the line and see how close to a triangle this really is?
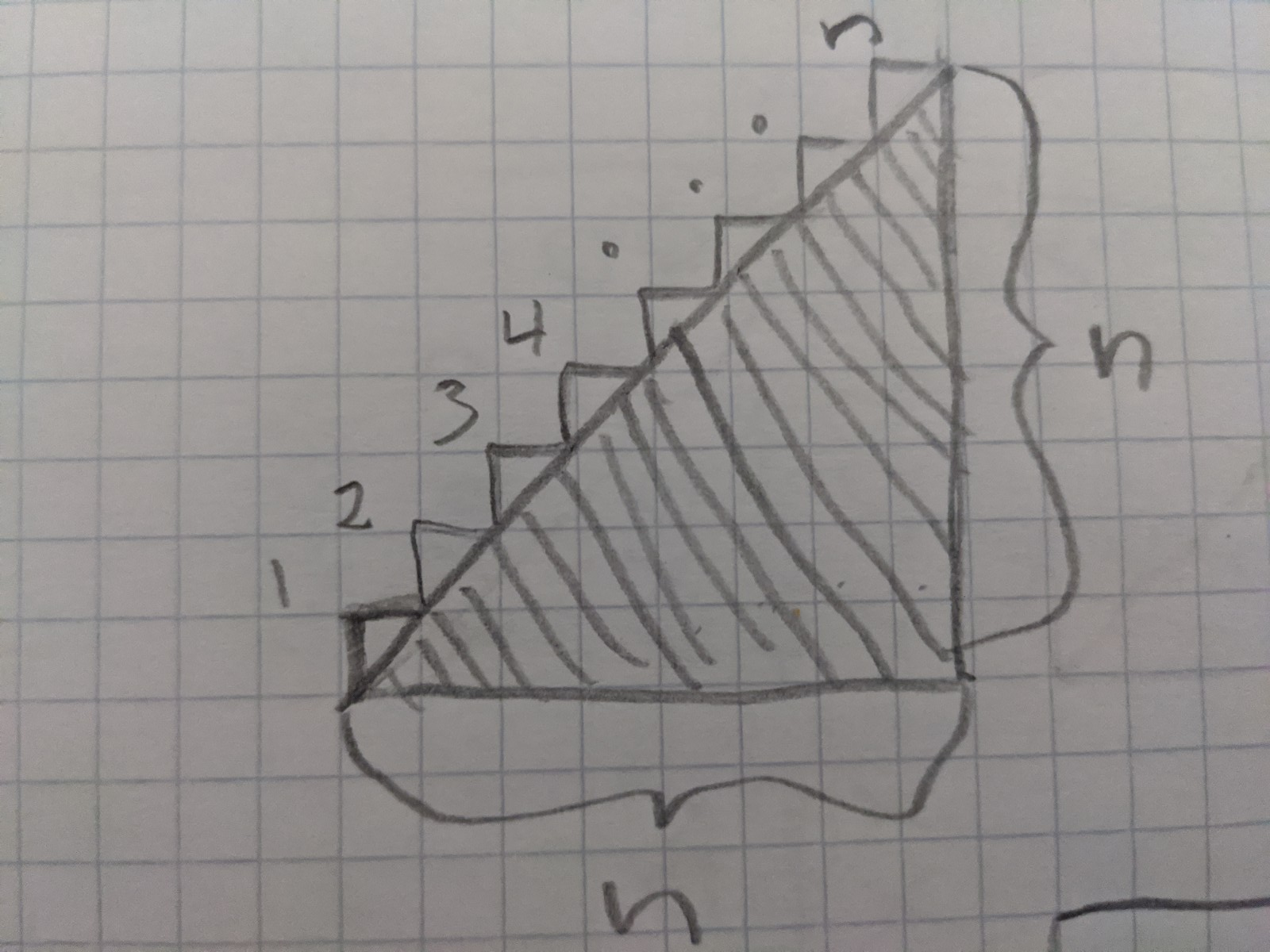
With the line drawn, it clearly seems there is one very large triangle with a right angle and 2 sides that each measure n units, and n little triangles with a right angle and 2 sides that each measure 1 unit. so
area of 1 n by n triangle + area of n 1 by 1 triangle
What’s the area of a triangle?
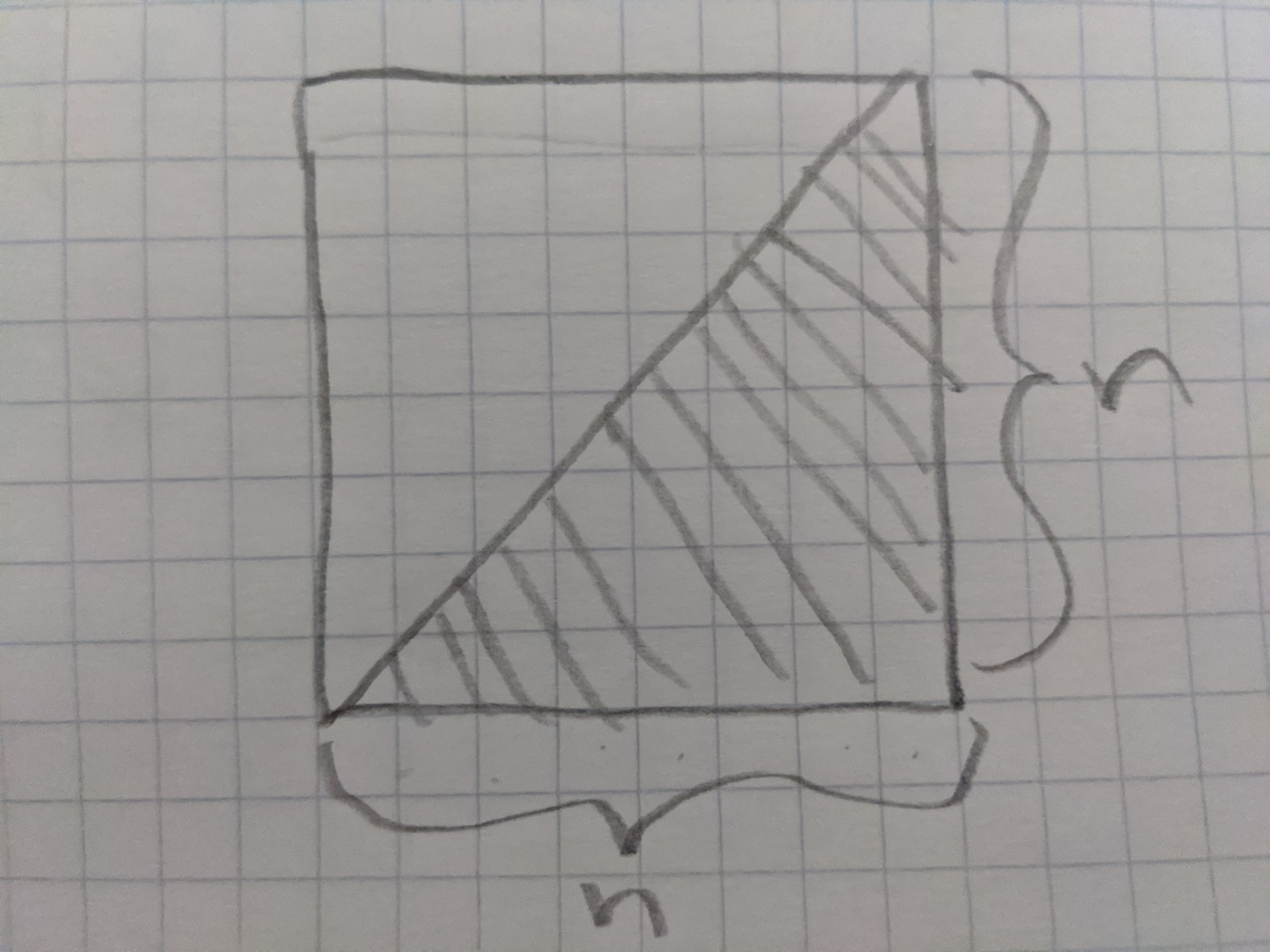
When you actually sketch it out and let your visual brain do the work its obvious that the area of the triangle is just one half of the area of a square that is n on each side.
(n * n * 1 / 2) + n * (1 * 1 * 1 / 2) = (n*n + n)/2 = n(n + 1)/2
So now we know how to calculate the sum of 1 + 2 + 3 + .. + n. Lets take apply what we have so far:
3 + 6 + 9 + 12 + 15 + … + 9,999,999 = 3 * floor((10,000,000-1)/3) * (floor((10,000,000-1)/3)+ 1) / 2
plus
5 + 10 + 15 + 20 + 25 + … + 9,999,995 5 * floor((10,000,000-1)/5) * (floor((10,000,000-1)/5) + 1) / 2
Are there any edge cases that we have to account for?
15 appears in both of these sequences, in fact every multiple of 15 is going to appear in both lists because 3 is a multiple of 15 and 5 is a multiple of 15. This can be resolved by subtraction the multiples of 15 less than 10,000,000 from our sum.
This seems like the answer and all i did to get there was ask myself questions.
By asking yourself the right questions at the right time you can raise your IQ by 20 points.
I often see developers cramming to master specific algorithms to nail interviews. I personally think that this information is great to know, but it’s more important to learn how to go about problem solving. A great resource to move from relying purely on intuition to solve problems into a more structured approach is the classic by How to Solve It by Poyla.

The last shall become first
In PowerShell our more sophisticated approach would look like:
$max = 10000000 - 1
$threes = 3 * ([math]::Floor($max / 3))*([math]::Floor($max / 3) + 1) / 2
$fives = 5 * ([math]::Floor($max / 5))*([math]::Floor($max / 5) + 1) / 2
$fifteens = 15 * ([math]::Floor($max / 15))*([math]::Floor($max / 15) + 1) / 2
$threes + $fives - $fifteens
Evaluating the performance of this is kind of difficult because it turns out just executing a completely empty PowerShell script takes orders of magnitude more time than calculating this value.
❯ hyperfine 'pwsh .\powershell\empty.ps1'
Benchmark #1: pwsh .\powershell\empty.ps1 0
Time (mean ± σ): 339.4 ms ± 5.4 ms [User: 0.0 ms, System: 5.7 ms] 1
Range (min … max): 333.6 ms … 351.3 ms 10 runs
PowerShell provides its own tooling to measure timing of commands called unoriginally enough, Measure-Command. Measure-Command will allow you to handily exclude the raw start up time of powershell executing an empty file from your benchmark. Also the faster languages like C# and Rust have a compilation step. It turns out PowerShell also has an implicit compilation step, the first time you execute something in PowerShell it is MUCH slower than subsequent executions. For this reason I am going to execute the statement 1 time, and then take the average of 10 runs of the PowerShell calculation being executed.
$max = 10000000
function calculate {
param($max)
$max = $max - 1
$threes = 3 * ([math]::Floor($max / 3))*([math]::Floor($max / 3) + 1) / 2
$fives = 5 * ([math]::Floor($max / 5))*([math]::Floor($max / 5) + 1) / 2
$fifteens = 15 * ([math]::Floor($max / 15))*([math]::Floor($max / 15) + 1) / 2
$threes + $fives - $fifteens
}
$compilePerformance = Measure-Command { calculate $max }
"First run: $($compilePerformance.TotalMilliseconds) ms"
1..20 |
Foreach-Object {
Measure-Command{ calculate $max }
} | Measure-Object -Property TotalMilliseconds -AllStats
❯ pwsh .\powershell\euler-math.ps1
First run: 14.4644 ms
Count : 10
Average : 0.7273
Sum : 7.273
Maximum : 5.7032
Minimum : 0.0586
StandardDeviation : 1.77348886911897
Property : TotalMilliseconds
So we are able to get approximately the same performance with our slowest language PowerShell (14.46 ms) as our fastest language Rust (15.5 ms) if we only look at intial execution. If we exclude the compilation step for each of these laguages, the gap in performance widens, with the algorithmically sophisticated PowerShell being about 20 times faster than the niave Rust implementation.
What did we learn?
Well really we just experimentally proved a couple old adadges in Computer Science/Programming.
Number 1 : Pretty much all modern programming langauges are fast enough. Even dirt slow PowerShell’s niave implementation clocking in around 2 minutes is probably less than the amount of time it would take implement the code, compile it and run it in the fastest language Rust. If you really just need the value one time they are all ‘fast’ enough.
Number 2 : If speed really does matter, applying an efficient algorithm to the bottlenecks of your system is going to have way bigger impact than just rewriting the whole thing in a fast language.
Number 3 : PowerShell is slow as hell
I leave off with the Gza Genius:
At the height of their fame and glory, they turned on one another
Each struggling in vain for ultimate supremacy
In the passion and depth of their struggle
The very art that had raised them to such Olympian heights was lost